こんにちは!引き続き統計学の記事を書いていこうと思います。本日は前回説明なしに使った度数分布表とヒストグラムについて解説していこうと思います。またそれに関連する用語の解説と演習問題も作成しましたので、よければ解いてみてください。
1. 度数分布表とは?
前回は用語だけ出して、ブログには書かなかったのですが、「度数分布表」とは何でしょうか?
データをいくつかの階級(範囲)に区切り、それぞれの階級にいくつデータが含まれるかを集計して一覧にした表になります。
さらに「度数」の説明をすると
その階級に含まれるデータ点の個数を度数と言います。
前回同様、10人のクラスがあって、100点満点のテストを実施したとしましょう。その点数が30点、25点、99点、28点、46点、19点、23点、80点、27点、84点
このデータを点数ごとに何人いるかの1点ごとに書こうとすると、
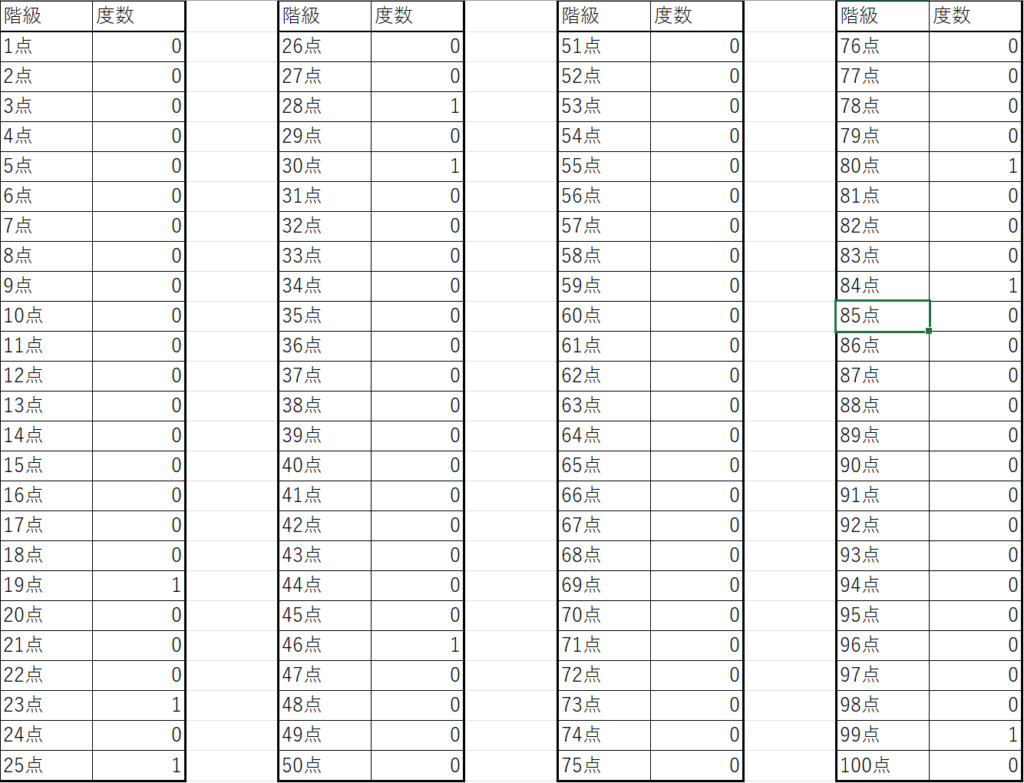
上記のような度数分布表になります。人数も10人程度しかいなくほとんどの階級の度数が0となっています。それに何より、どの点数帯に何人いるかわかりにくいと思います。
そこで10点区切りで「0点以上10点未満」、「10点以上20点未満」、「20点以上30点未満」、「30点以上40点未満」、「40点以上50点未満」、「50点以上60点未満」、「60点以上70点未満」、「70点以上80点未満」、「80点以上90点未満」、「90点以上100点未満」の10個の点数範囲にしてみましょう。
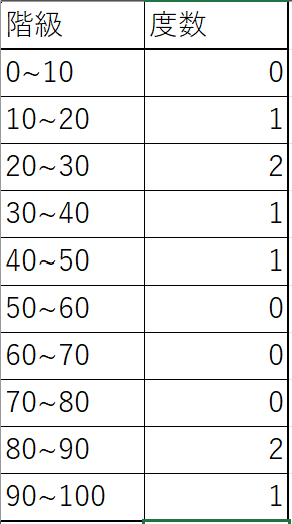
まだ見えにくいですが、多少マシな形になりましたね。このテストの受験者がとても多い場合には1点区切りで度数分布表を作成してもよいと思いますが、人数が少ない場合に受験者の傾向を知りたい場合には、このように階級を区切ってデータを作成する必要があるのです。
ここで、階級数値が10区切りであることを「階級の幅が10である」というので覚えておきましょう。
☆統計を極めたい方向け
なんとなく学校の学習内容だけ知っておきたい方は、この部分は読まなくて大丈夫です。
階級を何等分して度数分布表を書いたらよいか、わからない場合もありますよね?その際には経験則的にこれぐらいで書くとちょうどいいという「階級数を求める公式」があります。
それが「スタージェスの公式」です。定義は
ここではkを階級数、nをデータの個数とします。
つまり上記の例を用いると、階級数kは
このようになり、階級数は4か5を採用すればよいということになります。(あくまでグラフが美しく見える目安を決めているので、どちらを採用すればよいか悩んだ場合にはどちらも書いて美しく見える方を採用してください。)
今回k = 5を採用したとすると「0点以上20点未満」、「30点以上40点未満」、「40点以上60点未満」、「60点以上80点未満」、「80点以上100点未満」この5つの階級に分ければ傾向をなんとなくつかめるということがわかるかと思います。
2. ヒストグラムとは?
度数分布表が記述出来たら、次は「ヒストグラム」を書きましょう。
ヒストグラムとは「データをいくつかの区間(階級)に分け、その度数を棒グラフ形式で表したグラフ」となります。要は度数分布表を図にしてより直感的に理解しやすい形にしたものになります。
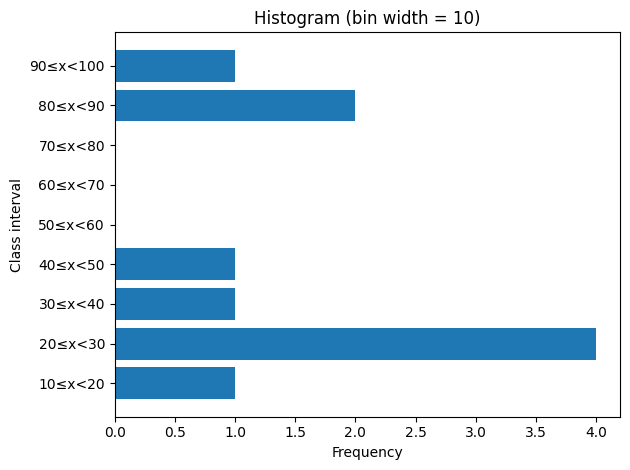
上記の例を階級の幅が10となるように記述したグラフになります。このグラフを見ると「このテストは中間層がいなく難しい問題が多そうかな?」という印象を受けると思います。
3. 演習問題
次の数学テスト(100点満点)の結果をもとに、
- 階級幅10点(0~9, 10~19, …, 90~99, 100)の度数分布表を作りなさい
- その度数分布表を使ってヒストグラムを作りなさい
データ(30人分)
12, 18, 24, 27, 31, 35, 36, 39, 41, 43,
45, 47, 52, 54, 55, 58, 61, 63, 66, 68,
70, 73, 75, 77, 81, 83, 86, 90, 92, 97解答
問1 度数分布表
| 階級(点) | 度数 |
|---|---|
| 0以上10未満 | 0 |
| 10以上20未満 | 2 |
| 20以上30未満 | 2 |
| 30以上40未満 | 4 |
| 40以上50未満 | 4 |
| 50以上60未満 | 4 |
| 60以上70未満 | 4 |
| 70以上80未満 | 4 |
| 80以上90未満 | 3 |
| 90以上100未満 | 3 |
| 100以上110未満 | 0 |
| 合計 | 30 |
問2 ヒストグラム

コメント