統計学 その2

こんにちは！

引き続き統計学の内容を解説していきます。

本日の記事は「代表値」に関する求め方とその解釈の説明、演習をしていきます。

「平均値」「中央値」「最頻値」に関する知識を解説します。

1. 平均値(Mean)
2. 中央値(Median)
3. 最頻値(Mode)
まとめ
演習問題
演習問題の解答・解説

1. 平均値(Mean)

平均値とは「すべてのデータの数値の合計をデータの個数で割った数値」を指します。
例えばi番目のデータの数値を $x_{i}$ とすると、

\bar{x} = \frac{x_1 + x_2 + \dots + x_n}{n}

数学Ⅱ以降を学習されている方は

\bar{x} = \frac{1}{n}\sum_{i=1}^{n}x_i

こっちの方がなじみ深いかもしれませんね。

さて、数式の定義を説明しましたがこの値は解釈がとても重要な値だと思います。

意味としては「みんなに平等に分け直したら、1人あたりどれくらいになるか」という意味の代表値であると私は解釈しています。ここが誤解されやすいポイントなのですが、「多くの人が同じ値であるというわけではない」ということです。

ここで一つ例を考えてみましょう。

10人のクラスがあって、100点満点のテストを実施したとしましょう。その点数が30点、25点、99点、28点、46点、19点、23点、80点、27点、84点だったとしましょう。そうすると平均点が、

\bar{x} = \frac{30 + 25 + 99 + 28 + 46 + 19+ 23 + 80 + 27 + 84}{10} = 46.1点

このようになります。クラスの大半は20~30点台しか取れていないテストにも関わらず、一部の高得点者に平均点が引っ張られて、クラスの大半が40~50点ぐらい取れているような錯覚をさせる値となっています。

このように一部のデータが極端に高かったり、低かったりすると平均値は大きく動くことから「平均値だけではデータから読み取れることは少ない」ということがわかります。

2. 中央値(Median)

先ほどの平均値が「みんなに平等に分け直したら、1人あたりどれくらいになるか」とするなら、中央値とは「データのちょうど真ん中の順番にいる人は、どのぐらいの値なのか」を表す値になります。

これは、先ほどのデータを使って説明すると平均値との乖離が見られて面白いかもしれませんね。

30点、25点、99点、28点、46点、19点、23点、80点、27点、84点のデータを点数の低い順に並び変えてみましょう。

19　23　25　27　28　30　46　80　84　99

このように点数が低い順に並べ替えることができました。

そうしたら、次に10人いるので、これを上位50%と下位50%となるように分ける場所を探してみてください。ちょうど28点と30点の間で区切ると１～５番目のグループと６～10番目のグループに分けられることがわかるかと思います。

「中央値」はその分けるところの真ん中の値を取ります。つまり

中央値 = \frac{28 + 30}{2} = 29点

ということです。平均値と違い、データのちょうど真ん中の人の点数を取ることができるため、より実態に近い数字を取ることができるようになりました。

ここで解釈としては、「外れ値(データの実態から大きく外れている値)の影響を受けにくい値である」という解釈ができると思います。平均値は約46点だったのに対し、「29点以上取れていればクラスの半分以上の成績である」と主張する中央値はこのクラスの実態をより明確に表現している値であるともとらえることができるかと私は思います。

3. 最頻値(Mode)

本日の記事の説明の最後は「最頻値」になります。最頻値とは最も多く登場した「値」や「階級」を表す値になります。

今回の例ですと、これを10点区切りの「度数分布表」に直してから、その「階級値」をそのデータの最頻値として決定しようと思います。

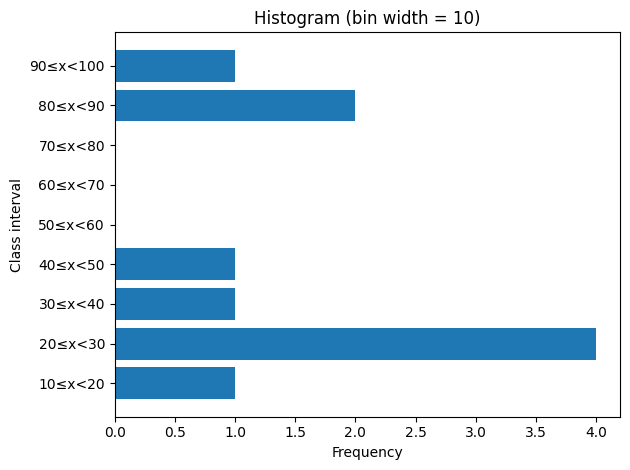
適当にmatplotlibを利用して、度数分布表を書いてみました。(Pythonを使ったので、プログラミングも興味があれば一緒に学習すると統計をより一層楽しめると思います。)

横軸が「度数」でその階級に含まれる人数になります。縦軸が各階級を並べたものになります。ここではわかるように「20点～29点の間に含まれる人数」が最も多く4人となるので、度数が最も多い階級の階級値である「25点」が最頻値となります。

ここからわかる「最頻値」の解釈としては「どの値にデータが偏るのかを表した値」と解釈するのが最もしっくりくると私は思っています。ただ、注意点としてデータの個数が少ない統計を取る場合には注意が必要だと思います。

今回ヒストグラムに直した理由としては、そのままのデータを利用すると最頻値が決まらないからです。元の19　23　25　27　28　30　46　80　84　99というデータは一つとして同じ値がありませんでした。それも当然でテストは同じ点数帯でも1点違うだけで最頻値は同じ値ではないと主張してしまいます。

たとえば10点満点のテストをするときに10人の結果が

3点、3点、3点、7点、8点、8点、9点、9点、10点、10点

としてみましょう。最頻値は「3点」ですが、なんとなく8～10点にデータが偏っているという気がすると思います。それもそのはずで平均点は「7点」、中央値は「8点」とこれだけ見たら高得点を取れて当たり前のテストに見えるはずです。

このように、最頻値は「どこにデータが最も集中しているか」を表す指標ではありますが、
その集中のしかたを必ずしも正確に表してくれるとは限らないという点に注意が必要です。

特に、

データの個数が少ない場合
点数が細かく分かれている場合
1点刻みで値がばらけやすいテストの場合

には、最頻値は直感とズレやすくなります。

今回の10点満点の例でも、
「3点」が最頻値であることは事実ですが、
それだけを見ると「低得点が多いテストだった」と誤解してしまいかねません。
しかし、実際には8点以上を取っている人が多く、
平均や中央値を見れば、全体としては高得点寄りの分布であることが分かります。

まとめ

つまり、
これらの代表値は「1つの数字」だけを見ると、データ全体の姿を見誤ることがあるのです。

そのため、統計では

最頻値
平均値
中央値

を必ずセットで考えることが重要になります。
さらに、今回のように ヒストグラムを使うことで、
「どのあたりに点数が集まっているのか」を視覚的に捉えることができます。

最頻値とは、
「この数字が一番多い」という単純な答えではなく、
データがどのあたりに偏っているかを考えるためのヒントとして使うものだ、
と考えると、よりしっくりくるのではないでしょうか。

演習問題

あるクラスで行った 100点満点の数学テストの結果が、次のようになりました。

42, 45, 48, 50, 52,
55, 58, 60, 60, 62,
65, 68, 70, 72, 75,
78, 80, 80, 80, 85

（全部で20人）

問1

このデータの
① 平均値
② 中央値
③ 最頻値
を求めなさい。

演習問題の解答・解説

① 平均値

合計は

42+45+48+50+52
+55+58+60+60+62
+65+68+70+72+75
+78+80+80+80+85
= 1285

人数は20人なので

平均値=1285÷20=64.25

② 中央値

データはすでに小さい順に並んでいます。

20個のデータなので、
10番目と11番目の平均を取ります。

10番目：62
11番目：65

中央値=(62+65)÷2=63.5

③ 最頻値

最も多く出てくる値を調べると、

60：2回
80：3回

最頻値は 80

統計学その2